Go to Problem

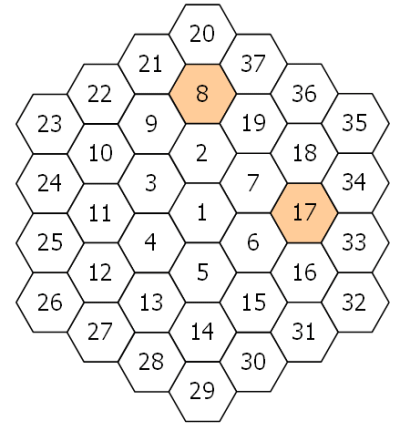
Summary

It’s easy since I spent only 2+ hours. So try it before read my thought and you’ll have some fun.

1. 1, 2, 8, 19 are the first 4 valid numbers.
2. Consider each ring as 6 vertex and many other nodes in edge.
3. Consider the series of vertice in direction 2, It’s 1, 2, 8, 20, ….

• We know every number in a ring if we know it first vertex in the previous series. For example, the 3rd rind is:

  $$20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37,$$

1. Every node has 2 neighbors which are in the same ring. For example, 10 and 12 are neighbors of 11, their difference is always 1 (10 - 11, and 12 - 11) which are not primes. So except the first and last node in a ring, all nodes have at least 2 neighbors are not primes.

2. Consider all vertice in 3, 5, 7 directions. The series in each direction is interleave with odd and even number, for example: [3, 10, 23, 42, …] is [odd, even, odd, even, …]. Now let’s check 10, it’s next vertex neighbor is 23, which is odd, and neighbors of 23 in it’s ring is 22, 24, which are evens, then 10 has 2 more difference which are not primes (even - even). We can find the same property in odd vertex. All of them have ate least 4 non-primes neighbors (2 + property 4).

3. Consider all vertice in 4 and 6 directions. They are all even which provide 2 non-prime neighbor difference.

4. Consider all edge nodes. They all have 2 neighbors from both outer and inner rings. For example, 11 has [3, 4] and [24, 25], 2 even and 2 odd which means no matter the node is even or odd, it’s 4 neighbors give it at least 2 more non-prime neighbor difference.

5. So, all we have to do is checking vertex in direction 2 (2, 8, 20, 38, ….) and the last node in each ring (7, 19, 37, 61, …).

Code in Python

from sympy import isprime


# 1, 2, 8, 19
L = 2000
T = 4
S = [1, 2, 8, 19]

a = 8
b = 20
c = 38
d = 62

k = 3

while len(S) < L :
    # first and last
    if isprime(abs(b - c + 1)) :
        if isprime(abs(b - c - 1)) and isprime(abs(b - d + 1)):
            S.append(b)

        if isprime(abs(c - 1 - a)) and isprime(abs(c - d + 1)) :
            S.append(c - 1)

    a, b, c, d = b, c, d, d + d - c + 6


print(S[L - 1])